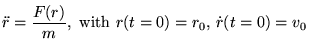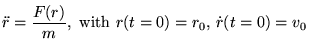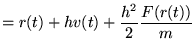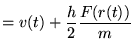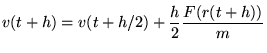De differentiaalvergelijkingen voor de enkele en dubbele (gekoppelde) slinger kunnen alleen in de harmonische benadering exact opgelost worden. Gebruikmakend van numerieke methoden kunnen deze echter met willekeurig kleine fout opgelost worden voor elke waarde van 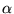 en
en 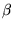 .
.
De methode die in de simulatie gebruikt wordt om numeriek te integreren heet het velocity Verlet algoritme. Dit algoritme is waarschijnlijk het meest gebruikte algoritme. Eerst wordt het gewone Verlet algoritme besproken.
De bewegingsvergelijking van Newton voor een deeltje met massa 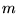 onderhevig aan een kracht
onderhevig aan een kracht 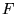 is:
is:
De Taylor benaderingen voor 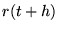 en
en 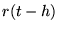 zijn:
zijn:
Optellen van (3) en (4) geeft:
herschikken:
Dit is het verlet algoritme.
De snelheid (
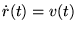 ), kan uitgerekend worden met:
), kan uitgerekend worden met:
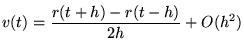 |
(6) |
Het gebruik van vergelijking (6) heeft een nadeel. Het heeft een fout van 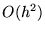 in plaats van de
in plaats van de 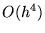 fout van (5). Als de snelheid erg belangrijk is (bijvoorbeeld om de kinetische energie te bepalen om energie behoud te kunnen controlleren) is het gebruik van het zogenaamde velocity Verlet algoritme aan te raden.
fout van (5). Als de snelheid erg belangrijk is (bijvoorbeeld om de kinetische energie te bepalen om energie behoud te kunnen controlleren) is het gebruik van het zogenaamde velocity Verlet algoritme aan te raden.
Eerst worden 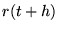 en
en 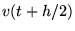 bepaald met de krachten op tijd
bepaald met de krachten op tijd 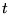 :
:
daarna wordt de kracht op 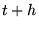 berekend met de nieuwe positie en wordt deze gebruikt om
berekend met de nieuwe positie en wordt deze gebruikt om
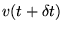 te berekenen:
te berekenen:
Deze vergelijkingen laten zich eenvoudig generaliseren, zodat ze ook te gebruiken zijn in systemen van bewegingsvergelijkingen.
Velocity Verlet met aanpassende stapgrootte
De stapgrootte moet klein genoeg gekozen worden om energiebehoud te garanderen gedurende de duur van het experiment. Het velocity Verlet algoritme met aanpassende stapgrootte wordt gebruikt om een geschikte stapgrootte te schatten. Dit algoritme schat de fout per integratiestap en past zijn stapgrootte hieraan aan.
In deze simulatie zal het algoritme toegepast worden op 1 periode van een enkele slinger. De kleinste stap die het algoritme kiest tijdens deze periode, zal gebruikt worden als stapgrootte voor de gehele simulatie (met de gekoppelde slingers). Het algoritme kan als volgt worden afgeleid:
Een simulatie van een deeltje met massa 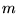 onderhevig aan een kracht
onderhevig aan een kracht 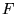 start op tijd
start op tijd 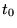 met een bekende positie
met een bekende positie 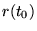 . Eerst wordt 1 integratie stap gedaan om de positie
. Eerst wordt 1 integratie stap gedaan om de positie
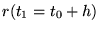 met een fout
met een fout 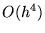 te schatten, deze benaderde positie wordt
te schatten, deze benaderde positie wordt 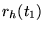 genoemd. De fout in deze stap is gedefinieerd als:
genoemd. De fout in deze stap is gedefinieerd als:
Aangezien de orde van de fout 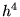 is, zal het nemen van een half zo grote stap resulteren in een fout die ongeveer
is, zal het nemen van een half zo grote stap resulteren in een fout die ongeveer 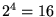 keer kleiner is. Twee stappen zijn dan nodig om
keer kleiner is. Twee stappen zijn dan nodig om 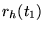 te schatten, dus de fout is:
te schatten, dus de fout is:
en ook:
Er is dus een benadering voor
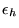 gevonden, ten koste van 2 extra stappen van
gevonden, ten koste van 2 extra stappen van 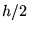 .
.
Kies een maximale fout
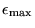 voor de gehele simulatie. Beginnend op
voor de gehele simulatie. Beginnend op 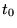 wordt er 1 integratiestap
wordt er 1 integratiestap 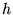 gedaan om
gedaan om 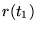 te benaderen. De positie
te benaderen. De positie 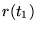 wordt ook benaderd door 2 stappen
wordt ook benaderd door 2 stappen 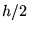 te doen. Beide resultaten worden vergeleken om een schatting voor
te doen. Beide resultaten worden vergeleken om een schatting voor
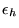 te krijgen. Met deze fout wordt de maximaal te nemen stapgrootte
te krijgen. Met deze fout wordt de maximaal te nemen stapgrootte
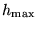 behorende bij
behorende bij
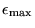 geschat:
geschat:
(vanwege de 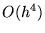 fout).
fout).
Als
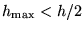 , dan zal
, dan zal 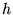 worden vervangen door
worden vervangen door
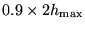 , en zal de integratie worden herhaald op
, en zal de integratie worden herhaald op 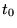 . De nieuwe stapgrootte wordt vermenigvuldigd met 0.9 om er zeker van te zijn dat de stapgrootte altijd klein genoeg is.
. De nieuwe stapgrootte wordt vermenigvuldigd met 0.9 om er zeker van te zijn dat de stapgrootte altijd klein genoeg is.
Als
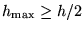 dan zal de stapgrootte klein genoeg zijn en zal de simulatie verder gaan naar
dan zal de stapgrootte klein genoeg zijn en zal de simulatie verder gaan naar 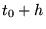 (waar
(waar 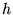 vervangen kan zijn bij de vorige stap).
vervangen kan zijn bij de vorige stap).
In de meeste toepassingen van dit algoritme wordt de stapgrootte ook vergroot als deze te klein is vergeleken met
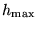 . Bij deze simulatie wordt dit niet gedaan omdat we juist de kleinste stap
. Bij deze simulatie wordt dit niet gedaan omdat we juist de kleinste stap
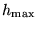 willen hebben die gebruikt is tijdens de simulatie. Dit zorgt er namelijk voor dat de simulatie (in het geval van de gekoppelde slingers) altijd wordt gedaan met een fout kleiner of gelijk aan
willen hebben die gebruikt is tijdens de simulatie. Dit zorgt er namelijk voor dat de simulatie (in het geval van de gekoppelde slingers) altijd wordt gedaan met een fout kleiner of gelijk aan
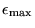 . Elke keer dat parameters van de simulatie veranderd zijn voor het starten ervan, wordt het algoritme gebruikt om de stapgrootte te schatten.
. Elke keer dat parameters van de simulatie veranderd zijn voor het starten ervan, wordt het algoritme gebruikt om de stapgrootte te schatten.
De stapgrootte die nodig is om zeker te zijn van redelijk energiebehoud is zo klein dat de simulatie niet per integratiestap naar het scherm wordt getekend. De simulatie wordt ongeveer 10 keer per seconde getekend.