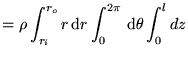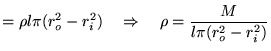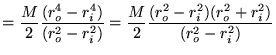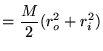As you can read here, the moment of inertia of an object with density 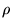 :
:
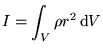 |
(21) |
This integral can be worked out for a hollow cylinder rotating around its symmetry axis:
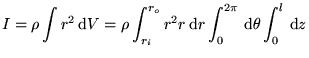 |
(22) |
after integration:
![$\displaystyle I = 2\pi l \rho \left[ \frac{r^4}{4}\right]_{r_i}^{r_o} = \frac{\pi l \rho (r_o^4-r_i^4)}{2}$](img-en/img63.png) |
(23) |
If we would want to compare 2 cylinders having the same mass, but with another inner and outer radius, we would have to write 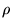 as a function of the mass
as a function of the mass 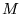 :
:
The moment of inertia can also be written as a function of mass instead of density:
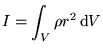
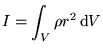
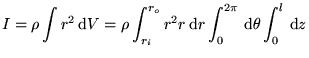
![$\displaystyle I = 2\pi l \rho \left[ \frac{r^4}{4}\right]_{r_i}^{r_o} = \frac{\pi l \rho (r_o^4-r_i^4)}{2}$](img-en/img63.png)