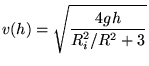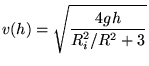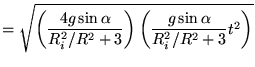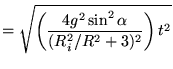Voor de volledigheid controleren we of beide methodes hetzelfde antwoord geven.

De methode op basis van behoud van energie, gaf ons:

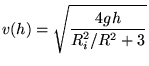$\displaystyle v(h) = \sqrt{ \frac{4gh}{R_i^2/R^2+3 }}$ (29)

Hier merken we op dat deze vergelijking geldt voor alle waarden van 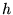$ h$. De vergelijking kan daarom herschreven worden als functie van $ x$:

$\displaystyle v(x) = \sqrt{ \frac{4gx\sin\alpha}{R_i^2/R^2+3 }}$ (30)

Oplossen van de bewegingsvergelijking gaf ons een vergelijking voor de snelheid als functie van de tijd:

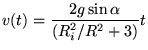$\displaystyle v(t) = \frac{2g\sin\alpha}{ \left(R_i^2/R^2+3 \right)}t$ (31)

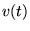Als we $ v(t)$ integreren naar de tijd:

$\displaystyle x(t) = \int_0^t v(t')\d t' = \frac{2g\sin\alpha}{ \left(R_i^2/R^2... ...right)} \int_0^t t' \d t'<BR> = \frac{g\sin\alpha}{ \left(R_i^2/R^2+3 \right)} t^2$ (32)

krijgen we $ x$ als functie van de tijd, wat we kunnen invullen in $ v(x)$:

$\displaystyle v(x(t))$ $\displaystyle = \sqrt{ \left(\frac{4g\sin \alpha}{R_i^2/R^2+3 }\right) x(t)}$    
  $\displaystyle = \sqrt{ \left(\frac{4g \sin \alpha}{R_i^2/R^2+3 }\right) \left(\frac{g\sin\alpha}{R_i^2/R^2+3 }t^2 \right)}$    
  $\displaystyle = \sqrt{ \left(\frac{4g^2\sin^2 \alpha}{(R_i^2/R^2+3)^2 }\right)t^2 }$    
  $\displaystyle = \frac{2g\sin \alpha}{R_i^2/R^2+3} t$ (33)

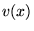Dit levert weer vergelijking 31.