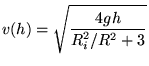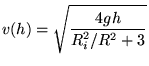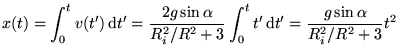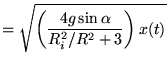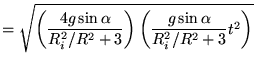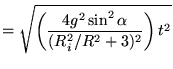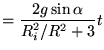For completeness we compare both methods.

The method based on conservation of energy resulted in:

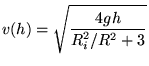$\displaystyle v(h) = \sqrt{ \frac{4gh}{R_i^2/R^2+3 }}$ (28)

We note that this equation applies to all values of 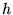$ h$. Therefore we can rewrite it as a function of $ x$:

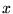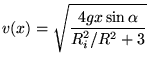$\displaystyle v(x) = \sqrt{ \frac{4gx\sin\alpha}{R_i^2/R^2+3 }}$ (29)

Solving the equation of motion resulted in:

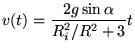$\displaystyle v(t) = \frac{2g\sin\alpha}{ R_i^2/R^2+3 }t$ (30)

Integrate 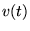$ v(t)$:

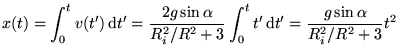$\displaystyle x(t) = \int_0^t v(t')\d t' = \frac{2g\sin\alpha}{ R_i^2/R^2+3 } \int_0^t t' \d t'<BR> = \frac{g\sin\alpha}{ R_i^2/R^2+3 } t^2$ (31)

Substitute 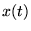$ x(t)$ into equation 30:

$\displaystyle v(x(t))$ $\displaystyle = \sqrt{ \left(\frac{4g\sin \alpha}{R_i^2/R^2+3 }\right) x(t)}$    
  $\displaystyle = \sqrt{ \left(\frac{4g \sin \alpha}{R_i^2/R^2+3 }\right) \left(\frac{g\sin\alpha}{R_i^2/R^2+3 }t^2 \right)}$    
  $\displaystyle = \sqrt{ \left(\frac{4g^2\sin^2 \alpha}{(R_i^2/R^2+3)^2 }\right)t^2 }$    
  $\displaystyle = \frac{2g\sin \alpha}{R_i^2/R^2+3} t$ (32)

Which results in equation 31.